- ホーム>SSLサーバ証明書とは
- 公開鍵暗号
公開鍵暗号
公開鍵暗号とは
暗号化通信を実現するためには、通信の当事者だけが共有する暗号化・復号化のための鍵が必要です。この鍵を「共通鍵」と呼びます。現実世界では、「共通鍵」を事前に共有する方法はたくさんありますが、インターネット通信では鍵の共有も通信でしかできず、その段階では暗号化されていない平文の通信経路を使っているわけですから、秘密裏に鍵を共有するのは簡単ではありません。
平文のインターネット通信経路を使って秘密裏に「共通鍵」を共有する方法として確立している技術が「公開鍵暗号」です。
「公開鍵暗号」では「公開鍵」と「秘密鍵」という二つの鍵をセットとして使います。この二つの鍵の内、「公開鍵」は制限なく公開・配布されます。一方秘密鍵は所有者以外閲覧できません。そして、「公開鍵」で暗号化されたデータは「秘密鍵」だけで復号化できるという特殊な関係が成立します。
http 通信で「公開鍵暗号」を使って秘密裏に「共通鍵」を共有する一例を非常に簡略化して説明すると以下のようになります。
- サーバーはリクエストしてきたブラウザに、SSLサーバー証明書を送ります。SSLサーバー証明書には「公開鍵」が含まれています。
- ブラウザは鍵になる文字列を決め、サーバーから受け取った「公開鍵」で文字列を暗号化し、サーバーに送ります。
- サーバーは暗号化された文字列を「秘密鍵」を使って復号化し、ブラウザが決定した元の文字列を入手します。
上記の過程は http 通信で行われているので第三者が傍受することができますが、ブラウザから送られた暗号化されたデータは、「秘密鍵」を持っているサーバーだけしか復号化できないので、傍受されても心配ありません。
このようにして、「公開鍵暗号」を使って、平文のインターネット通信経路を使って秘密裏に「共通鍵」を共有することができます。
この鍵交換の過程を「ハンドシェイク」と呼びます。詳しくは「ハンドシェイク」のページを参照ください。
公開鍵暗号の種類
1976年に、ラルフ・マークルの研究の影響を受けたウィットフィールド・デフィーとマーティン・ヘルマンが公開鍵暗号に関する世界最初の論文を発表し、公開鍵暗号という概念が知られるようになりました。
翌、1977年にはロナルド・リベスト、アディ・シャミア、レオナルド・エーデルマンによって最初の公開鍵暗号・RSA暗号が発明されました。RSAの名称は発明者である3人の頭文字に由来しています。
公開鍵暗号には「DH (Diffie-Hellman)」、「RSA (Rivest-Shamir-Adleman)」、「DSA (Digital Signature Algorithm)」、「楕円曲線暗号 (ECC: Elliptic Curve cryptosystem)」がありますが、「暗号化」、「署名」、「鍵交換」の機能を持つのは「RSA暗号」と「楕円曲線暗号」でこの二つがSSLサーバー証明書で利用できます。
RSA暗号
現在、楕円曲線暗号の SSLサーバー証明書も少数利用されていますが、ほとんどの SSLサーバー証明書でRSA暗号が使われています。
RSA暗号は素数がもつ特性を利用して公開鍵暗号を実現しています。
公開鍵暗号・RSA暗号を可能にした素数がもつ特性
暗号化前の整数を m とします。m を e 乗した数字を、二つの素数の積(p x q)で剰余した結果を、暗号化された数字 c とした場合、 暗号化された数字 c を d 乗し、二つの素数の積(p x q)で剰余すると暗号化前の整数 m が得られる。
me mod (p x q) = c cd mod (p x q) = md は以下の計算で求められます。i は整数です。
d = (i × (p - 1) x (q - 1) + 1)/e
この特性を利用してRSA暗号の秘密鍵と公開鍵が作られています。
公開鍵には p,q の積と e だけが情報として提供されます。
秘密鍵は p,q,e,d の値が保存されています。
実際に小さな数字でこの特性を検証してみましょう。
-
公開鍵で暗号化し、秘密鍵で復号化する
p, q, e m me mod (p x q) c (i × (p - 1) x (q - 1) + 1)/e d cd mod (p x q) m p = 3, q = 11, e = 3 15 153 mod (3 x 11) 9 (1 x (3 - 1) x (11 - 1) + 1)/3 7 97 mod (3 x 11) 15 p = 3, q = 11, e = 3 24 243 mod (3 x 11) 30 (1 x (3 - 1) x (11 - 1) + 1)/3 7 307 mod (3 x 11) 24 -
秘密鍵で暗号化し、公開鍵で復号化する
p, q, d, e m md mod (p x q) c ce mod (p x q) m p = 3, q = 11, d = 7, e = 3 15 157 mod (3 x 11) 27 273 mod (3 x 11) 15 p = 3, q = 11, d = 7, e = 3 24 247 mod (3 x 11) 18 183 mod (3 x 11) 24
RSAの秘密鍵と公開鍵を作ってみる
実際にRSAの秘密鍵と公開鍵を作って上記の特性を確認してみます。正規の秘密鍵は2048bit以上で作成しますが、桁数が大きくなりすぎで電卓では特性の検証が不可能になってしまいますので36bitで作成します。
openssl コマンドで秘密鍵を作成します。
# openssl genrsa 36 > private.key Generating RSA private key, 36 bit long modulus .+++++++++++++++++++++++++++ .+++++++++++++++++++++++++++ e is 65537 (0x10001)
秘密鍵から公開鍵を作成します。
openssl rsa -in private.key -pubout -out public.key writing RSA key
秘密鍵の内容は以下となっています。
# openssl rsa -in private.key -text -noout Private-Key: (36 bit) modulus: 46845590359 (0xae836fb57) publicExponent: 65537 (0x10001) privateExponent: 27137696161 (0x6518861a1) prime1: 235007 (0x395ff) prime2: 199337 (0x30aa9) exponent1: 143305 (0x22fc9) exponent2: 93121 (0x16bc1) coefficient: 44623 (0xae4f)
同様に公開鍵の内容は以下となっています。
openssl rsa -pubin -in public.key -text -noout Public-Key: (36 bit) Modulus: 46845590359 (0xae836fb57) Exponent: 65537 (0x10001)
prime1 (235007) が上記説明数式の p に該当します。
prime2 (199337) が上記説明数式の p に該当します。
modulus (46845590359) が上記説明数式の p x q (235007 x 199337) に該当します。
publicExponent, Exponent (65537) が上記説明数式の e に該当します。
privateExponent (27137696161) が上記説明数式の d に該当します。
d = (i × (p - 1) x (q - 1) + 1)/e については、i = 37966 とすると成立します。
27137696161 = (37966 x (235007 -1) x (199337 -1) + 1)/65537
RSAの秘密鍵と公開鍵を使ってみる
鍵長より大きなデータの暗号化ができないので以下のコマンドで、鍵長 2048 bit の秘密鍵と公開鍵を新規に作成します。
openssl コマンドでまず、秘密鍵を作成します。
# openssl genrsa 2048 > long_private.key Generating RSA private key, 2048 bit long modulus ............................................................................................................................+++ ......+++ e is 65537 (0x10001)
秘密鍵から公開鍵を作成します。
openssl rsa -in long_private.key -pubout -out long_public.key writing RSA keyこの公開鍵と秘密鍵を利用して、opennssl コマンドで文章の暗号化と復号化を行ってみます。
文章は「I'm fine.」としこれを original.txt に保存します。暗号化した文章を crypted.txt に保存することにします。
復号化した文章を decrypted.txt に保存することにします。
以下のコマンドを実行します。
暗号化
# openssl rsautl -encrypt -pubin -inkey long_public.key -in original.txt -out crypted.txt
復号化
openssl rsautl -decrypt -inkey long_private.key -in crypted.txt > decrypted.txt
original.txt、crypted.txt、decrypted.txt の内容は以下となり、正しく復号化されていることが確認できました。
# cat original.txt I'm fine. # hexdump crypted.txt 0000000 5798 c03a 45d8 5b95 9a39 714b 9f6b 4254 0000010 ca3a 7537 4641 0032 0e81 8876 0bed f7e1 0000020 3c58 d92b 42f4 0787 1608 a763 8822 8695 0000030 973b bab2 fde5 456b 56d8 1924 cd7e 903b 0000040 3486 5ca7 1fcb 4b7b 0fec abb8 5160 9c82 0000050 95a1 93c8 a616 e4d5 ff14 564c 213f 477a 0000060 5b4f d2e8 c7e2 db6e 0858 c26d 7c89 d6dc 0000070 b4c9 1146 acf3 a325 43c5 2772 0c0c 6f09 0000080 3f04 33a8 8401 65be 84e0 6684 28b3 80eb 0000090 05b5 e29f dc82 949b 6eba 39c8 19c5 894d 00000a0 a9c4 3708 b0d1 91ea a55c f79c 6561 473c 00000b0 045c 4766 3d30 86d0 1898 1c9f 7fa2 9450 00000c0 4c5c f099 d9d5 1aec 1c12 cf96 0273 602e 00000d0 1563 c90a 31d5 6a8c 78c4 980b eac9 7d1f 00000e0 27b2 7e1a 4aa0 6d25 a741 5b9a 469a e43c 00000f0 2461 5d87 e8fc 49e6 79de 314e 6ec7 d3e7 0000100 # cat decrypted.txt I'm fine.
楕円曲線暗号
楕円曲線暗号は、1985年にニール・コブリッツとビクタ・ミラーがそれぞれ別に提案されました。楕円曲線暗号は、現在SSLサーバー証明書や仮想通貨の鍵などに使われ、SSLサーバー証明書ではRSA暗号に代わる次世代証明書として注目されています。
楕円曲線暗号はRSA暗号と比べると1/10程度の鍵長でRSA暗号と同程度の強度を持つとされています。そのため、処理速度が格段に速くなります。
楕円曲線暗号証明書はWebサーバーでは Apache、Nginx、IISなどの主要サーバーで利用可能です。またブラウザではChrome、Firefox、IE、Edge、Safariなどの主要ブラウザが対応しています。
楕円曲線暗号の原理
楕円曲線暗号は「楕円曲線離散対数問題の困難性に依存する」と言われています。この原理をできるだけわかりやすく説明します。
y2 = x3 + ax +b上記の方程式は、楕円曲線を表しますが、a、bの値を適切に設定した場合以下のような曲線となります。
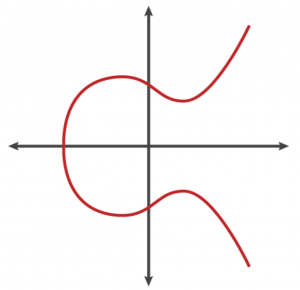
上記の方程式では、x、yは整数以外の値を取ることができますが、楕円曲線暗号ではx、yは大きな素数 q の剰余とします。そのことは、以下ののように表現されます。
E: y2 Ξ x3 + ax +b mod q
楕円曲線上のある点AとBを加算した点は下図のDになります。点Aと点Bを結んだ直線が曲線が交わった点が-D、その垂線と曲線が交わった点がDです。
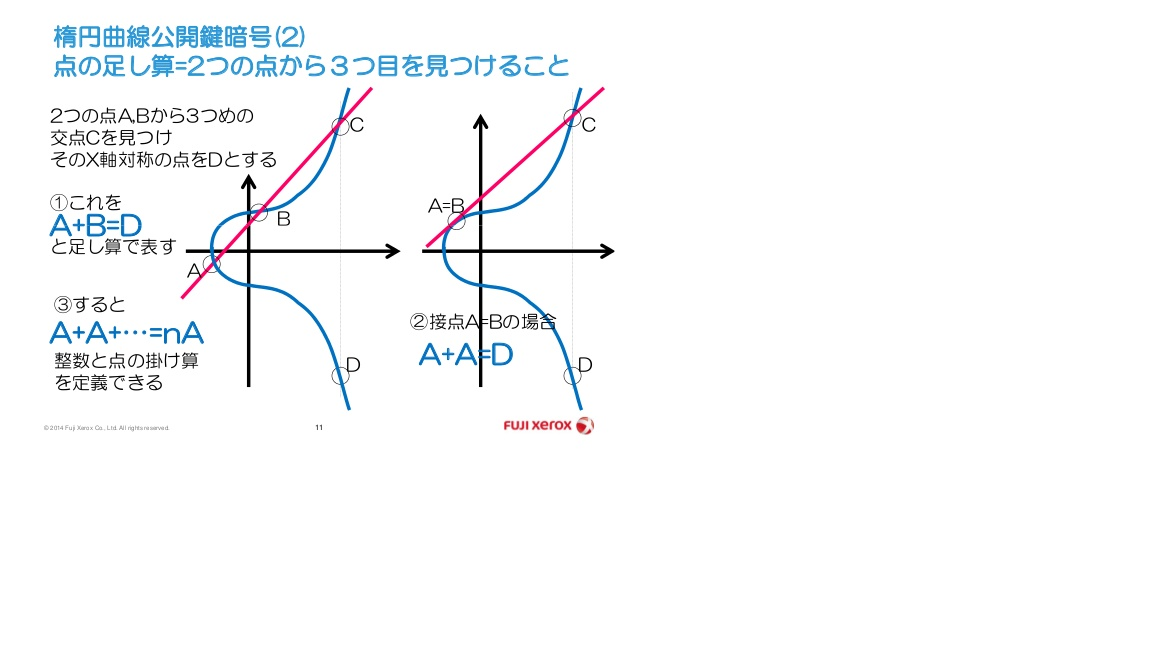
楕円曲線上のある点Gを2倍した点は下図の2Gになります。点Gでの曲線の接戦と曲線が交わった点が-2G、その垂線と曲線は交わった点が2Gです。
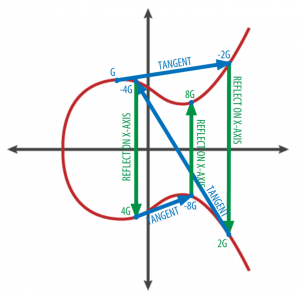
同様の作業を繰り返すとnG を得ることができます。n が一定数以上になると、「y2 Ξ x3 + ax +b mod q」とGの値、nGの値が分かっていても、nの値を求めることは困難です。このことを「楕円曲線離散対数問題の困難性」といいます。
そのため、nの値を秘密鍵として利用し、nGの値を公開鍵として利用することができます。